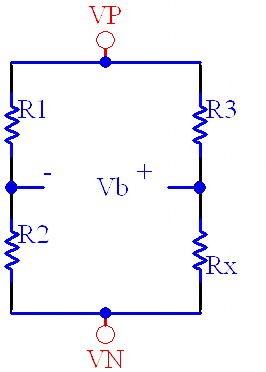
The Wheatstone bridge (also known as the single-arm bridge) is an instrument that can accurately measure resistance. Figure 3-13 shows a general Wheatstone bridge. Resistors R1, R2, R3, and R4 are called the four arms of the bridge, and G is a galvanometer, which is used to check whether there is current in the branch where it is located. When no current passes through G, the bridge is said to be balanced. When balanced, the resistance values ​​of the four arms satisfy a simple relationship, which can be used to measure resistance.

The bridge voltage is calculated as follows:

V_B=  V_in*[Rx/(R3+Rx)- R2/(R1+R2)]

If R3=R1, and Rx= R2+delta, then

V_B=  V_in*[ (R2+delta)/(R1+R2+delta)-R2/(R1+R2)]

Now, if we assumedeltais smaller than R1 + R2, then

V_B= ~ V_in*[delta/(R1+R2)]

Thus, we can see that the bridge voltage is approximately proportional to the errordelta, divided by the sum of the resistances on one side.

Given the bridge voltage, we can calculate the value of an unknown resistor.

(R1+R2)*(R3+Rx)*V_B/V_in= Rx*(R1+R2)+ R2*(R3+Rx)

Rx*(R1+R2)*V_B/ V_in +  R3* (R1+R2)V_B/V_in= Rx*R1+Rx*R2 - R2*R3- Rx*R2

Rx*R1 - Rx*(R1+R2)*V_B/ V_in  = R2*R3 + R3* (R1+R2)V_B/V_in

Rx = (R2*R3 + R3* (R1+R2)V_B/V_in )/ (R1- (R1+R2)*V_B/ V_in)